STRATÉGIE DU CARRÉ

Le plan actuel du rez-de-chaussée fait émerger un constat, la relation entre ce qui a existé et ce qui a été créé ultérieurement n’est pas naturelle. La création de la veranda pour accéder à l’extension marque la rupture et amplifie le sentiment de passer au dehors pour revenir au dedans. La maison n’est plus une maison mais un assemblage d’espaces.


Ce sentiment se retrouve dans la proportion des pièces. Le salon est grand, la cuisine initiale est trop petite pour être fonctionnelle. La création de l’extension trouve ainsi son utilité dans le but de remédier à ce déséquilibre. Cependant, si la nouvelle cuisine est grande, elle se retrouve au fond de la maison alors qu’elle devrait être au début.

Allant au bout de la démarche, l’escalier du salon se retrouve également en doublon dans la cuisine de l’extension et trouve sa logique dans cette fuite en avant ou plutôt en arrière de la dite recomposition de l’espace.


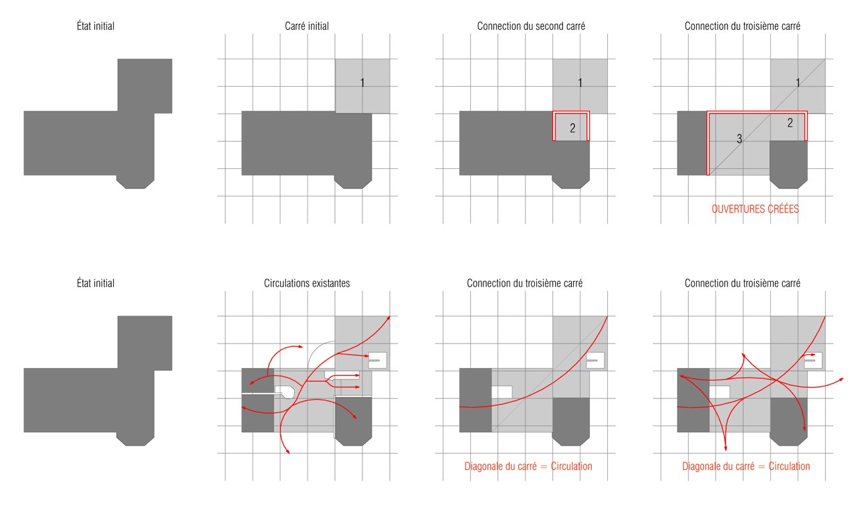
Cette analyse nous a conduit à développer un raisonnement à rebours, un processus à l’envers afin de réorganiser l’espace intérieur. L’extension se présente en plan sous la forme d’un carré et c’est de cet espace que le process inverse s’est construit.

En effet, en réappliquant le même principe de doublon, nous avons cherché à les annuler, à créer des opposés qui ensemble recomposent une unité. Il a alors été intéressant de constater que la théorie du double carré renvoie au théorème de Pythagore et à la « Géométrie sacrée ».


L’intérêt de cette recherche réside dans le fait que les proportions et longueurs des segments sont conséquentes les unes des autres. Ainsi à partir du premier carré, nous avons remonter le processus de Pythagore qui consiste à établir qu’un triangle est rectangle si et seulement si ses deux côtés au carré sont égales à l’hypothénuse au carré. 

En effet, en réappliquant le même principe de doublon, nous avons cherché à les annuler, à créer des opposés qui ensemble recomposent une unité. Il a alors été intéressant de constater que la théorie du double carré renvoie au théorème de Pythagore et à la « Géométrie sacrée ». 

L’intérêt de cette recherche réside dans le fait que les proportions et longueurs des segments sont conséquentes les unes des autres. Ainsi à partir du premier carré, nous avons remonter le processus de Pythagore qui consiste à établir qu’un triangle est rectangle si et seulement si ses deux côtés au carré sont égales à l’hypothénuse au carré. 


Théorème de Pythagore

Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.


Réciproque du théorème de Pythagore

Si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et l’angle droit est l’angle opposé au plus grand côté, et le plus grand côté de ce triangle est son hypoténuse.


Théorème de Pythagore
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.

Réciproque du théorème de Pythagore
Si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et l’angle droit est l’angle opposé au plus grand côté, et le plus grand côté de ce triangle est son hypoténuse.


ORG_0.html
ORG_0.html
MSL_0.html

STRATÉGIE DU CARRÉ = ESPACE + DISTRIBUTION

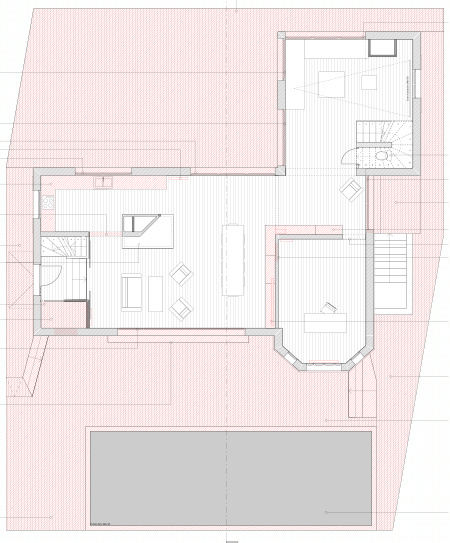
RDC APRÈS

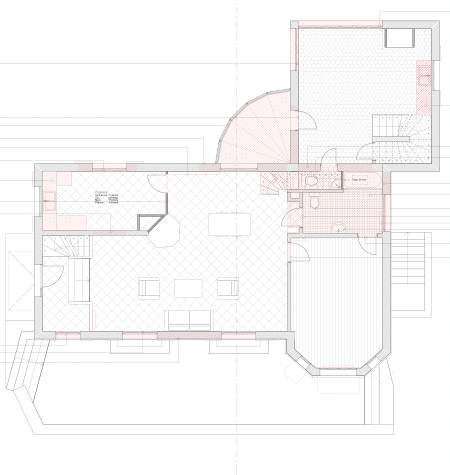
RDC AVANT

RÉHABILITATION DE MAISON

MONTIGNY SUR LOING

240m2

RÉALISÉ

2013

SITUATION

SURFACE

ETAT

DATE

LA DIAGONALE DU DOUBLE CARRÉ

PROJETS.html
PROJETS.html